2 逻辑代数

逻辑表达式A+BC=
1. B+C
2. A+C
3. (A+B)(A+C)
4. A+B
\(Y=A+\overline{B\overline{CD}}\) 的反函数是
1. \(\overline{Y}=\overline{A}\cdot \overline{\overline{B}+\overline{C}+\overline{D}}\)
2. \(\overline{Y}=\overline{A}\cdot \left( \overline{B}+\overline{C}+\overline{D} \right) \)
3. \(\overline{Y}=\overline{A}\cdot \overline{B+C+\overline{D}}\)
4. \(\overline{Y}=\overline{A}\cdot B\left( \overline{C}+\overline{D} \right) \)
\(L=\overline{A}\overline{B}+CD\) 的反函数是
1. \(\overline{L}=\left( \overline{A}\overline{B} \right) \cdot \left( CD \right) \)
2. \(\overline{L}=\left( AB \right) \cdot \left( \overline{C}\overline{D} \right) \)
3. \(\overline{L}=\left( A+B \right) \cdot \left( \overline{C}+\overline{D} \right) \)
4. \(\overline{L}=\left( \overline{A}+\overline{B} \right) \cdot \left( C+D \right) \)
函数 \( L=AB+B+BCD= \)
1. \(0\)
2. \(B\)
3. \(A+B\)
4. \(1\)
以下符合逻辑运算法则的是
1. 1+0=10（注：为二进制数）
2. 1+1=0（注：为二进制数）
3. A+1=1
4. C+C=C^2
当\(i≠j\)时，同一逻辑函数的两个最小项\(m_i \cdot m_j = \)
1. 1
2. 0
3. \( m_{i\times j} \)
4. \( m_{i+j} \)
\(n\) 变量的逻辑函数，\(m_i\) 为最小项，则所有 \(2^n\) 个最小项之和为
1. 0
2. \( 2^n \)
3. 1
4. n
使逻辑函数 \(L\left( A,B,C,D \right) =\overline{A}B+C\overline{D}\) 为1的最小项有几个？
1. 5
2. 6
3. 8
4. 7
若逻辑函数\(F(A,B,C)=\sum m(1,2,3,6)\)，\(G(A,B,C)=\sum m(0,2,3,4,5,7)\)，则F和G相与的结果为
1. \( \sum m(2,3) \)
2. 1
3. AB
4. 0
若逻辑函数\(F(A,B,C)=\sum m(1,2,3,6)\)，\(G(A,B,C)=\sum m(0,2,3,4,5,7)\)，则F和G相或的结果为
1. \( \sum m(2,3) \)
2. 1
3. AB
4. 0
已知\(F(A,B,C)=\sum m(3,4,6,7)\)，则\( \overline{F} = \)
1. \(\sum m(0,1,3,4)\)
2. \(\sum m(0,1,2,5)\)
3. \(\sum m(3,4,6,7)\)
4. \(\sum m(0,1,2,6)\)
逻辑函数\(L=A\oplus (A\oplus B)\)的结果为
1. A
2. \( A \oplus B \)
3. B
4. \( \overline{\overline{A}\oplus B} \)
求一个逻辑函数L的对偶式L'时，下列说法不正确的是
1. 把L中的"与”换成“或”，“或”换成“与”
2. 常数中的"1”换成"0"，"0”换成“1"
3. 原变量换成反变量，反变量换成原变量。
4. 保持原式中的运算顺序不变。
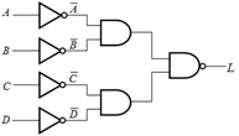
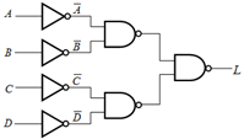
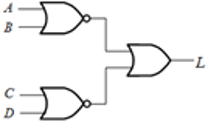
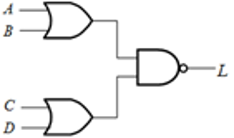
如果规定只能使用非门和2输入与非门来实现 \( L = \overline{(A+B)(C+D)} \)，则正确的逻辑图是：
下列不等式不成立的是
1. \(\overline{A}B+A\overline{B}+\overline{A}\overline{B}+AB=1\)
2. AB+AC+BC=AB+BC
3. A+AB=A
4. (A+B)(A+C)=A+BC
已知A+B=A+C，则B=C，对吗？
已知AB=AC，则B=C，对吗？
n个变量的最小项是包含全部n个变量的乘积项，在乘积项中每个变量只能以原变量的形式出现一次。对吗？
对偶式的反函数，就是原函数，对吗？
\(L(A,B,C)=AB+\overline{A}C\)的最小项是
1. \(\sum m(3,5,6,7)\)
2. \(\sum m(3,4,6,7)\)
3. \(\sum m(1,3,6,7)\)
4. \(\sum m(1,4,6,7)\)

Answer

最小项的编号：带非号的为0，不带非号的为1

C (A+B)(A+C) = AA+AC+AB+BC = A+AC+AB+BC = (A+AC+AB)+BC = A+BC，其中A+AC+AB=A 利用了吸收律。
D 分两步获得反函数：第一步：与、或互变：\(\overline{Y}=A\cdot \overline{B+\overline{C+D}}\)；第二步：原变量、非变量互变：\(\overline{Y}=\overline{A}\cdot \overline{\overline{B}+\overline{\overline{C}+\overline{D}}}\)，将其中\(\overline{\overline{B}+\overline{\overline{C}+\overline{D}}}\)利用反演法则进行改写为：\(B\cdot \left( \overline{C}+\overline{D} \right) \)，其中 \( \overline{C}+\overline{D} \) 看成一个整体。因此：\(\overline{Y}=\overline{A}\cdot B\left( \overline{C}+\overline{D} \right) \)，答案为D
C
B AB+B+BCD 中的第一、三项均被B吸收,AB+B+BCD=B,答案为B。
C A中+为加法,且有进位,并不是"或"; B中+为加法,且没有进位,并不是"或";C 正确；D错误,逻辑运算没有平方,应为C•C=C
B 任意两个不相同的最小项不会同时为1,它们相与为0,答案为B。
C 任意两个不相同的最小项不会同时为1,只能有其中某一个最小项为1。将所有最小项相加,即'或'操作,结果为1,答案为C。
D 将原式改写成最小项形式,其中 \( \overline{A}B \) 经扩充后,变成\(\overline{A}B\left( \overline{C}\overline{D}+\overline{C}D+C\overline{D}+CD \right) \),变为4项;CD ̅经扩充后,也变为4项,因此,共有8个最小项，其中1项重复，所以是7个最小项。7个最小项中的任意一个为1,L都会为1
A ∑m(1,2,3,6)和∑m (0,2,3,4,5,7)相与的时候,只有相同的最小项才能保留下来,否则相与的结果为0,所以只能m2和m3保留了下来。答案为A 。
B ∑m(1,2,3,6)和∑m (0,2,3,4,5,7)相'或'的时候,就等于最小项的相加,所有最小项都能保留下来,结果为∑m (0,1,2,3,4,5,6,7)=1。答案为1。
B \(\overline{F}=1-F=\sum m(0,1,2,3,4,5,6,7)-\sum m(3,4,6,7)=\sum m(0,1,2,5)\)
C A⨁B：两变量异或相当于A、B的二进制加法(因为AB不同时,加法结果一定为1,AB相同时,加法结果一定为0)。A⨁(A⨁B)三变量异或相当于A、A、B的二进制加法,其中A、A相加一定为0,所以结果为B。
C 对偶式就是"与/或"互变,"0/1"互变。但是变量并不变成反变量。答案是C。
B 首先进行变换,消除“或”门,保留“与”门。对两个括号内部,分别采用反演律：\(L=\overline{\left( A+B \right) \left( C+D \right) }=\overline{\left( \overline{\overline{A}\cdot \overline{B}} \right) \left( \overline{\overline{C}\cdot \overline{D}} \right) }\)，对应的电路图为B。
B A正确,所有最小项相加为1；B.错误,无法得出；C.正确,吸收律；D.正确,分配律+吸收律
False 此处加号为"或",不是真正的"加"。例如A=1时,等式成立,但是B可以不等于C。
False 此处为"与",不是真正的"乘"。例如A=0时,等式成立,但是B可以不等于C。
False 错，还可以以反变量的形式出现一次。
False 错，对偶式中的原变量、反变量没有互变。
C