6.4 典型时序逻辑电路
寄存器
存储器:存储二进制数据的逻辑单元。主要由触发器构成,1个触发器可存储1位二进制数据,存储n位二进制数据的寄存器需要用n个触发器组成。
典型芯片74HC374:片内输入、输出端缓冲电路用于与外部电路隔离,提高兼容性和驱动能力。
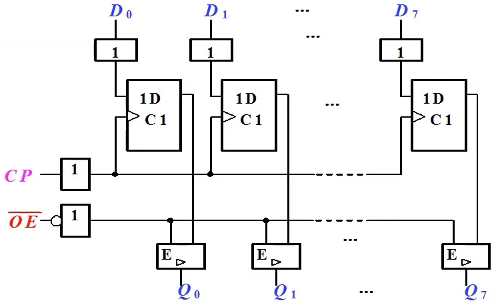
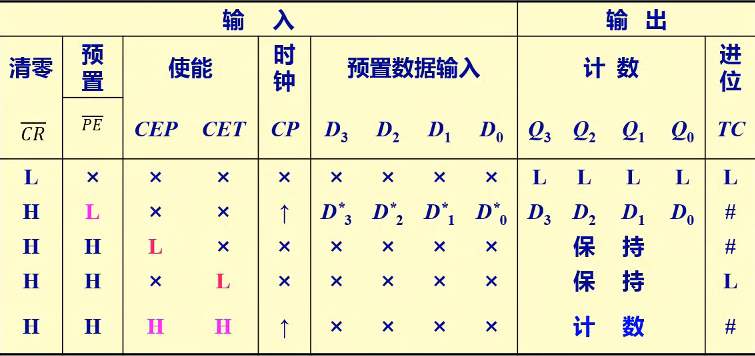
功能表(\(L^*\)和\(H^*\)表示CP脉冲上升沿之前瞬间\(D_N\)的逻辑电平)
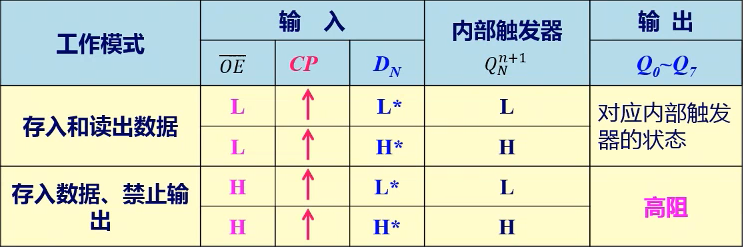
在CP上升沿的触发下,\( Q_N^{n+1}=D_N \)
\( \overline{OE} = L \),输出对应内部触发器的状态
\( \overline{OE} = H \),输出高阻态
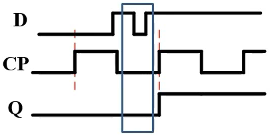
锁存器74HC/HCT373(由锁存器构成):
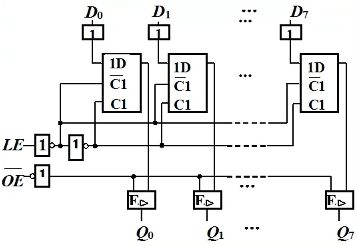
时钟电平触发,只要LE有效(H),输入随时刷新8个锁存器的状态。
寄存器74HC/HCT374(由D触发器构成):
脉冲边沿触发,只有在时钟边沿瞬间,同步更新触发器的状态。
移位寄存器
移位寄存器的逻辑功能:移位寄存器是既能寄存数码,又能在时钟脉冲的作用下使数码向高位或向低位移动的逻辑功能部件。
移位寄存器的逻辑功能分类(按移动方式分类):
单向移位寄存器:左移位寄存器、右移位寄存器
双向移位寄存器
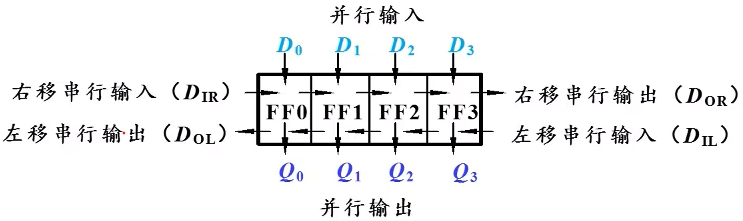
基本移位寄存器(右移寄存器)
规定(画图时左边低位,右边高位):左移:总是由高到低;右移:总是由低到高
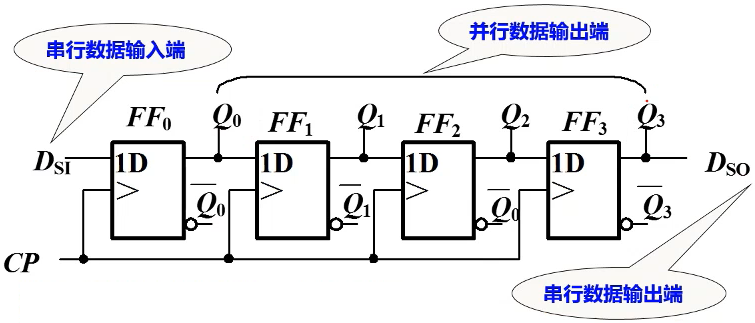
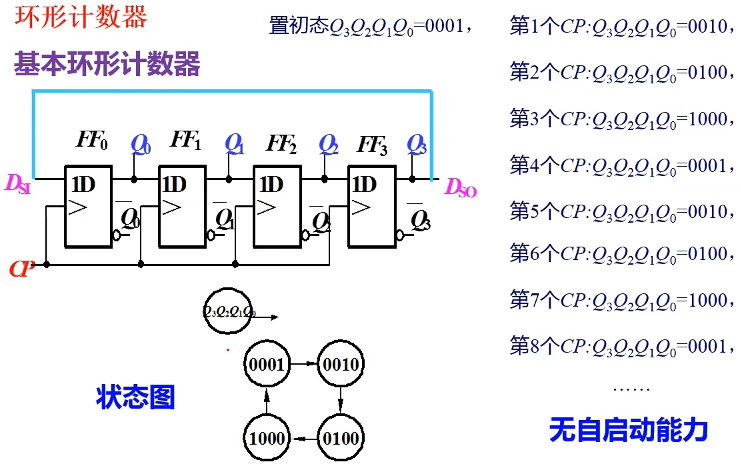
驱动方程:\( D_0 = D_{SI}, D_1=Q_0, D_2=Q_1, D_3=Q_2 \)
状态方程:\( Q_0^{n+1}=D_{SI}, Q_1^{n+1}=Q_0^n, Q_2^{n+1}=Q_1^n, Q_3^{n+1}=Q_2^n \)
实例: \(D_{SI} = 11010000\),从高位开始输入
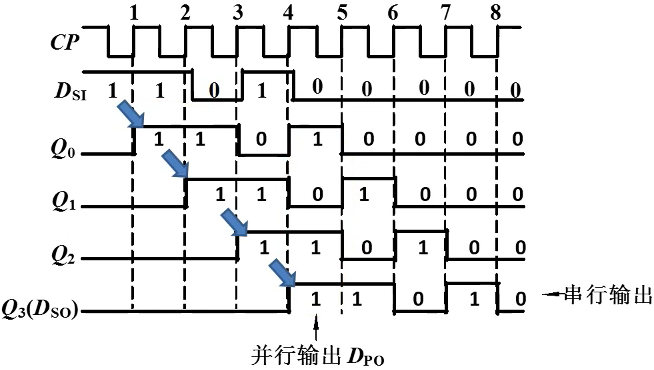
\(D_{SI}\) 端的串行输入从 \( Q_0,Q_1,Q_2,Q_3 \)并行输出,串入→并出
\(D_{SI}\) 端的串行输入从 \( D_{SO} \)串行输出,串入→串出
功能特点小结:
输入数码在CP控制下,依次右移或左移;
寄存n位二进制数码。n个CP完成串行输入,并可从\(Q_0\sim Q_{n-1}\)端获得并行输出,再经n个CP可在\(D_{SO}(Q_{n-1})\)端完成串行输出。
典型芯片:8位移位寄存器74HC/HCT164
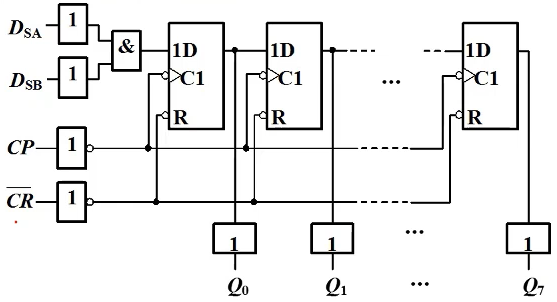
异步清零 (低电平有效);\( D_S=D_{SA}\cdot D_{SB}\rightarrow Q_0\rightarrow Q_1\rightarrow \cdots \rightarrow Q_7 \)
双向移位寄存器
右移:寄存器中的数据从低位触发器移向高位触发器;
左移:寄存器中的数据从高位触发器移向低位触发器(与计算机程序的规定相反)
基本原理:通过选择器实现左移或右移
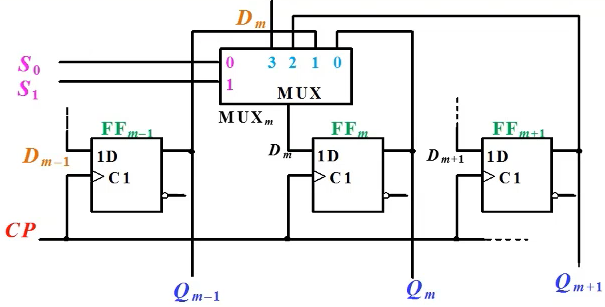
\( S_1S_0=00 \)
\( Q_{m}^{n+1}=Q_{m}^{n} \)
保持
\( S_1S_0=00 \)
\( Q_{m}^{n+1}=Q_{m-1}^{n} \)
右移
\( S_1S_0=00 \)
\( Q_m^{n+1} = Q_{m+1}^n \)
左移
\( S_1S_0=00 \)
\( Q_m^{n+1}=D_m \)
并行输入
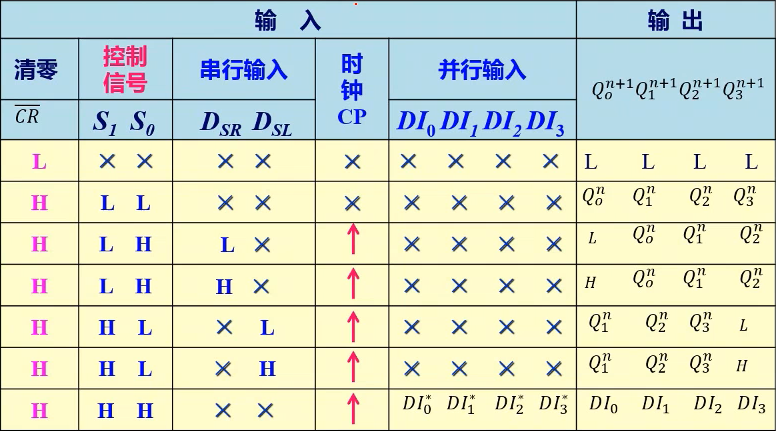
典型芯片:4位双向移位寄器74HCT194
计数器
计数器:计算时钟的脉冲个数,主要由T触发器构成。
计数器的模:计数器的容量,计数器的有效状态数等于模数。
功能:计数、分频、定时、产生脉冲序列以及某些数学运算。
计数器的分类:
按计数进制分类:二进制计数器、十进制计数器、N进制计数器
按计数方向分类:加法计数器、减法计数器、可逆计数器
按控制方式分类:同步计数器、异步计数器
异步二进制计数器
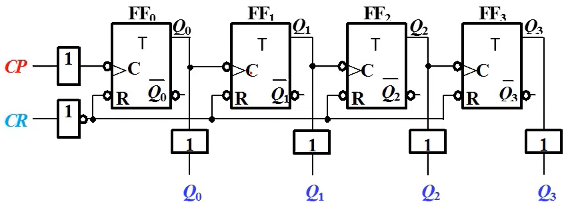
T触发器,图中下降沿触发,T=1翻转。
计数原理: 第六个下降沿过后,\( Q_3Q_2Q_1Q_0=0110=6_{(D)} \),实现计数
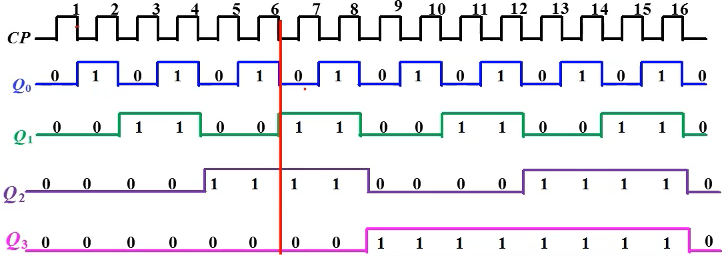
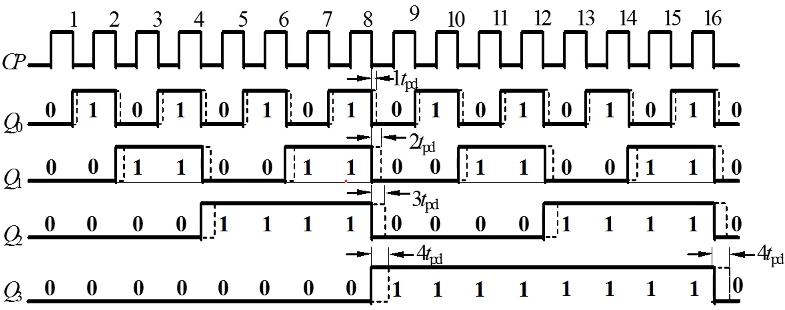
缺点: 延时大。假设每个触发器的延时者为\(t_{pd}\),则N位异步二进制计数器最高位的延时为\(Nt_{pd}\)。因此异步二进制计数器的脉冲周期必须满足\(T>Nt_{pd}\),否则将计数混乱 (这就限制了时钟频率不能过高) 。
典型芯片:74HC/HCT393(双4位异步二进制计数器)
同步二进制计数器
三位加计数器:

状态方程:\( Q_{0}^{n+1}=\overline{Q_{0}^{n}}, Q_{1}^{n+1}=Q_{0}^{n}\cdot \overline{Q_{1}^{n}}, Q_{2}^{n+1}=Q_{0}^{n}\cdot Q_{1}^{n}\cdot \overline{Q_{2}^{n}}, \cdots \),其中:\( T_0=1, T_1=Q_0^n, T_2=Q_0^n \cdot Q_1^n \)
由此得到n位二进制同步加计数器级联规律:
\( T_i=Q_{i-1}^{n}Q_{i-2}^{n}\cdots Q_{i}^{n}Q_{0}^{n}=\prod_{j=0}^{i-1}{Q_{j}^{n}} \)
触发器的状态刷新是同时进行的。高位\(Q_m^{n+1}\)不必等待低位\(Q_{m-1}^{n+1}\)进位才变化。
4位二进制同步加计数器
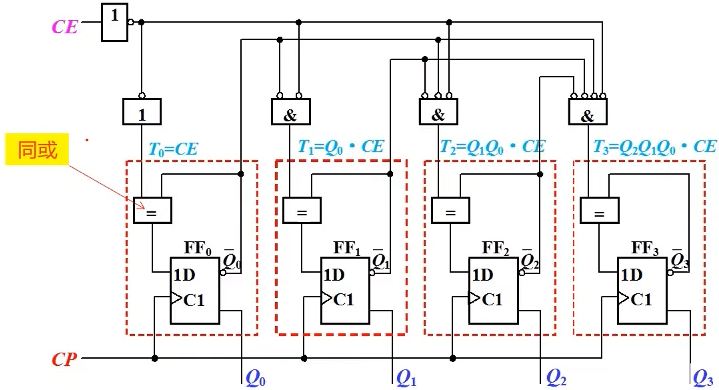
时序图:
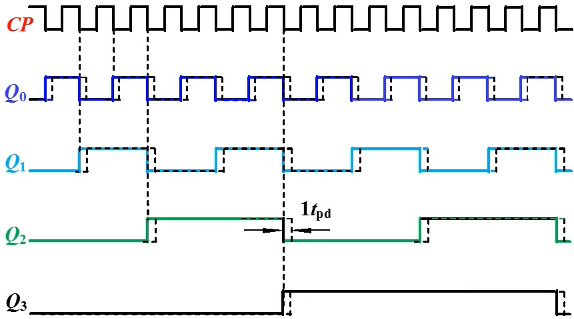
所有触发器同步刷新,都只比CP滞后一个\(t_{pd}\)
输出比异步二进制计数器稳定,工作速度快;
结构比异步二进制计数器复杂
典型芯片:74LVC161
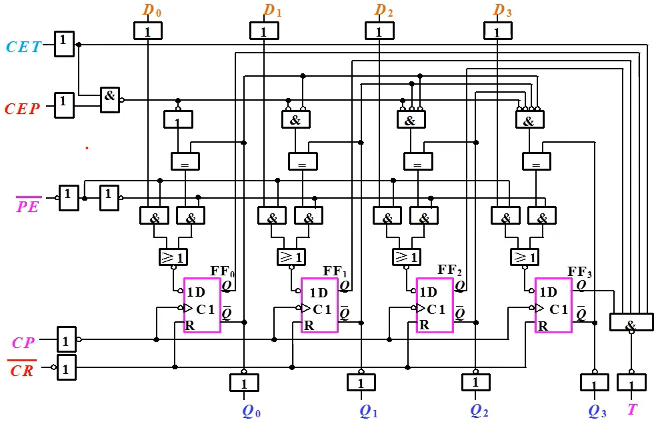
\(TC=CET\cdot Q_3Q_2Q_1Q_0\),不仅控制使能,也控制TC的输出。
74LVC161扩展实现16位计数:低进位标志作为使能信号,控制高位计数器的工作。
高位计数器只能在低位计数器TC为1时候,计数一次。
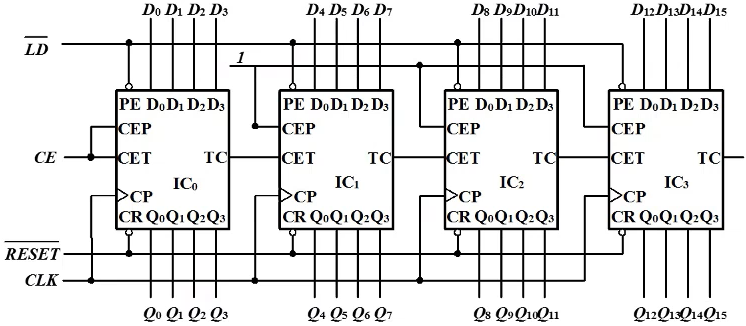
用集成计数器构成任意进制计数器
例:用74LVC161构成九进制加计数器。九进制计数器应有9个状态,而74LVC161在计数过程中有16个状态,应该设法跳过多余的7个状态。
反馈清零法
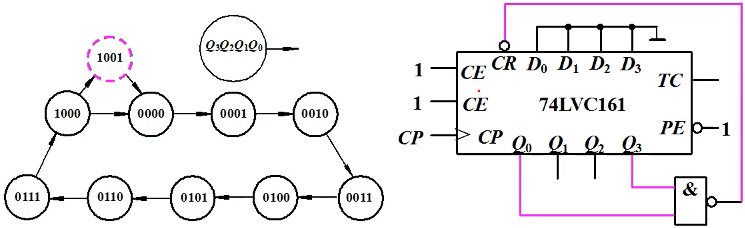
反馈置数法
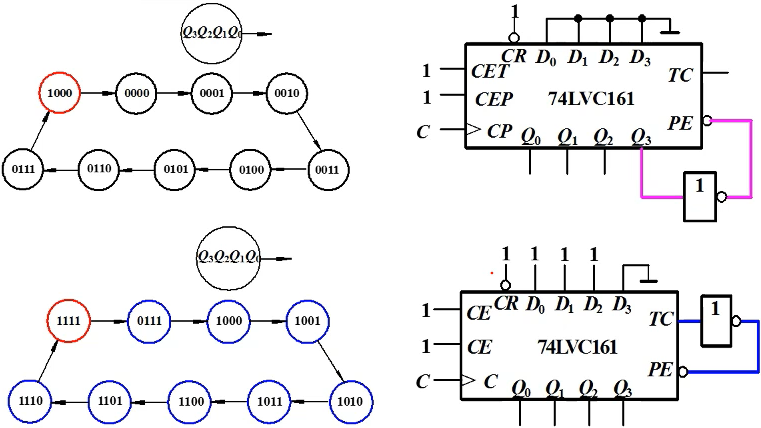
环形计数器