6.2 同步时序逻辑电路的分析
基本任务:根据逻辑电路图,找出电路状态的变化规律及输出信号的变化规律,最终确定电路的逻辑功能。
分析时序逻辑电路的一般步骤
写出逻辑方程:各触发器激励方程、各触发器特性方程→发触器状态转换方程、输出方程
列状态表,画状态图、时序图:状态方程、输出方程→状态转换图表
确定逻辑功能
米利型例题:分析图示时序电路逻辑功能(两个T触发器同步触发)
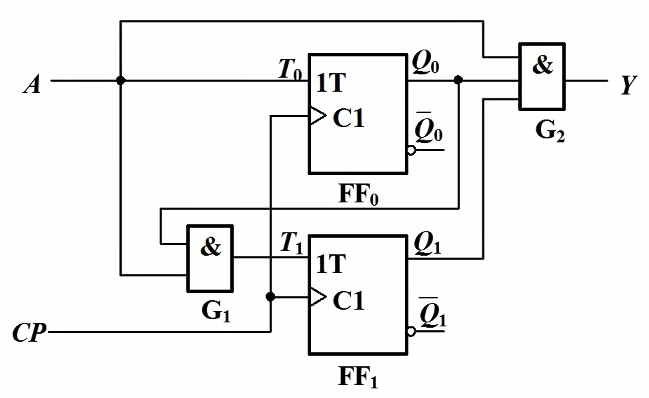
写出逻辑方程
激励方程组: \( T_0=A, T_1=AQ_0 \)
触发器特性方程: \( Q^{n+1}=T\oplus Q^n \)
状态方程组: \( Q_0^{n+1}=A\oplus Q_0^n, Q_1^{n+1}=(AQ_0^n)\oplus Q_1^n \)
输出方程组: \( Y=AQ_1Q_0 \)
状态表
\( Q_1^{n+1}Q_0^{n+1}/Y \)
\( Q_1^{n}Q_0^{n} \)
\(A=0\)
\(A=1\)
00(a)
00(a)/0
01(b)/0
01(b)
01(b)/0
10(c)/0
10(c)
10(c)/0
11(d)/0
11(d)
11(d)/0
00(a)/1
状态图
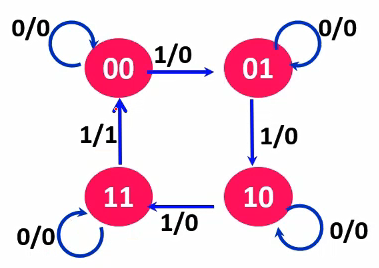
时序图(CP↑)
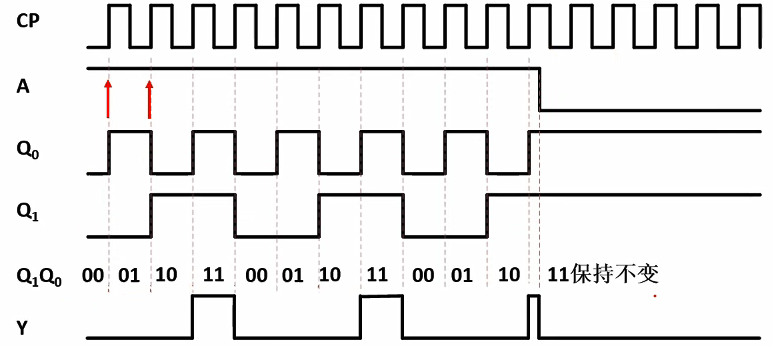
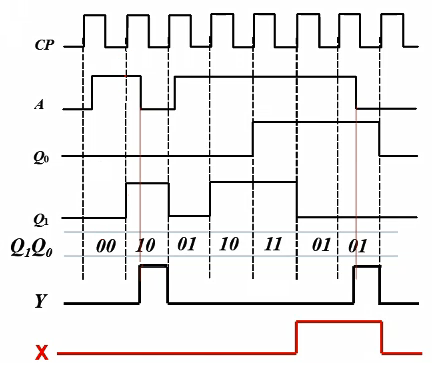
根据方程组/状态表/状态图画出状态时序图。
由输出方程/状态表/状态图画输出时序图。
功能分析:该电路是由信号A控制的2位二进制计数器,Y进位输出。
米利型电路易受干扰。输入端的任何抖动都会直接反映到输出端。
摩尔型例题:分析图示时序电路逻辑功能(三个D触发器同步触发)
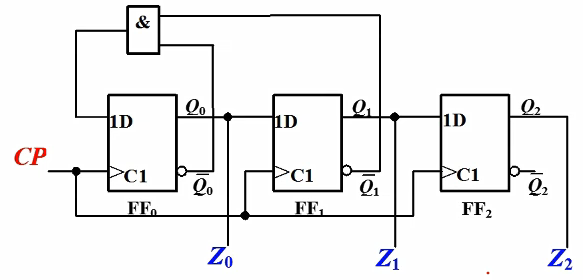
写出逻辑方程
激励方程组:\( D_0=\overline{Q_1}\cdot \overline{Q_0}, D_1=Q_0, D_2=Q_1 \)
触发器特性方程: \(Q^{n+1}=D\)
状态方程组:\( Q_{0}^{n+1}=D_0=\overline{Q_{1}^{n}}\cdot \overline{Q_{0}^{n}}, Q_{1}^{n+1}=D_1=Q_{0}^{n}, Q_{2}^{n+1}=D_2=Q_{1}^{n} \)
输出方程组: \( Z_0=Q_0, Z_1=Q_1, Z_2=Q_2 \)
状态表
\( Q_2^nQ_1^nQ_0^n \)
\( Q_2^{n+1}Q_1^{n+1}Q_0^{n+1} \)
000
001
001
010
010
100
011
110
100
001
101
010
110
100
111
110
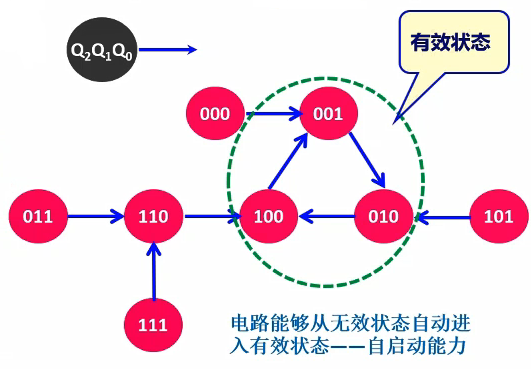
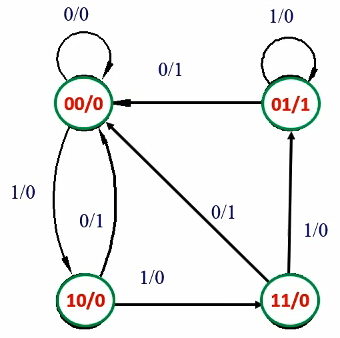
状态图
时序图(CP↑)
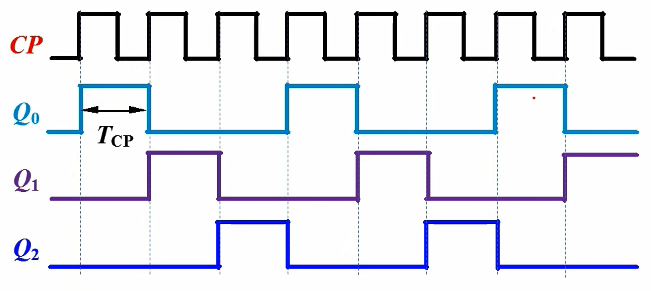
功能分析: 电路正常工作时,各触发器Q端轮流出现宽度为一个CP周期的脉冲信号,循环周期为\(3T_{CP}\)。该电路具有三位循环码计数功能,可用于脉冲分配或节拍脉冲产生。
混合输出分析例题:分析图示时序电路逻辑功能(两个D触发器同步触发)
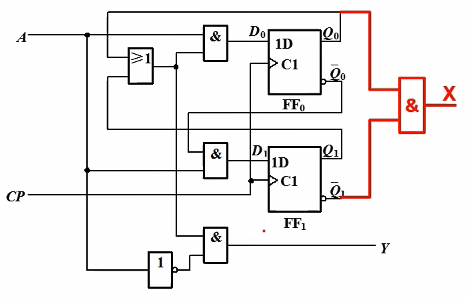
写出逻辑方程
激励方程组:\( D_0=(Q_0+Q_1)A, D_1=\overline{Q_0}A \)
触发器特性方程: \(Q^{n+1}=D\)
状态方程组:\( Q_{0}^{n+1}=D_0=\left( Q_{0}^{n}+Q_{1}^{n} \right) A, Q_{1}^{n+1}=D_1=\overline{Q_{0}^{n}}A \)
输出方程组: \( Y=\left( Q_0+Q_1 \right) \overline{A}, X=\overline{Q_1}Q_0 \)
状态转换真值表
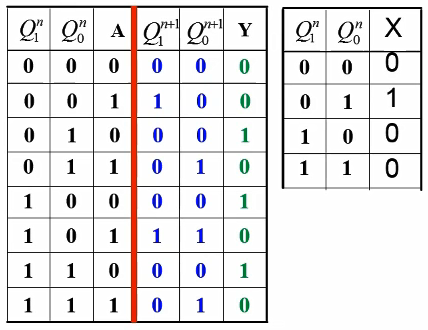
状态表
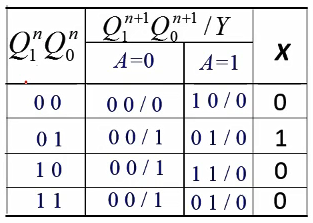
状态图
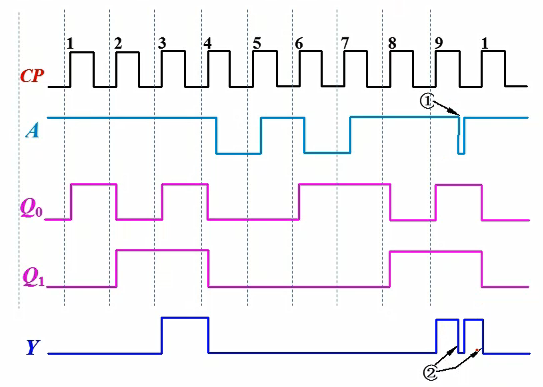
时序图(CP↑)