6.1 时序逻辑的概念和表示方法
组合逻辑电路:电路的输出状态只取决于同一时刻的输入,而与电路原来的状态无关。无反馈无记忆功能;由门电路构成。
时序逻辑电路:电路的输出状态不仅取决于同一时刻输入信号,而且与电路原来的状态有关。有反馈有记忆功能;由组合逻辑电路和存储电路构成。
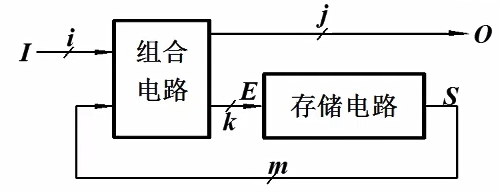
按存储单元状态变化特点分类:
同步时序电路:有一个统一的时钟脉冲信号CP,存储电路中各触发器的状态只在CP作用下才可能发生转换。
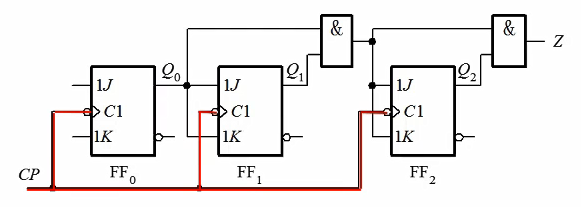
异步时序电路:没有统一时钟信号,各触发器状态变化不同步。
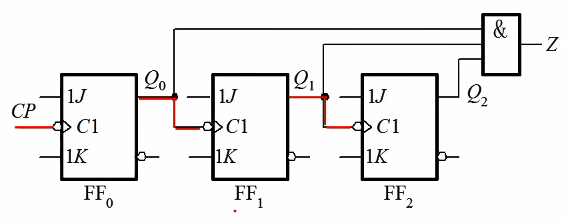
按输出信号的特点分类:
米利型 (Mealy) 时序电路: 输出由输入信号和存储状态共同决定\( Y=f(I,S^n) \)
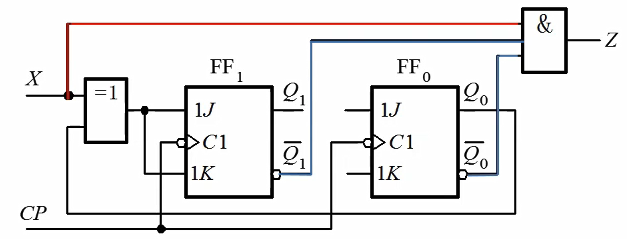
摩尔型 (Moore) 时序电路: 输出仅由存储状态决定,与当前输入没有关系 \( Y=f(S^n) \)
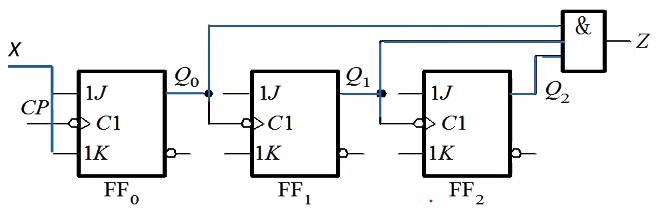
逻辑方程组描述:须用三个方程组才能完全描述其功能
变量表述:
输入信号I;
存储电路输入、激励信号E;
存储电路输出、状态信号/状态变量S;
输出信号O
驱动/激励方程组: 激励信号与输入信号、状态变量的关系式 \( E = g(I,S) \)
状态方程组: 存储电路从现态到次态的转换关系式 \( S^{n+1}=h(E,S) \)
输出方程组: 输出信号与输入信号、当前状态变量的关系式 \( O=f(I,S) \)
举例
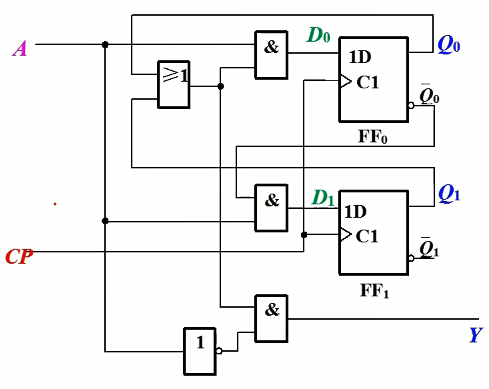
激励方程组: \( D_0=(Q_0+Q_1)A, D_1=\overline{Q_1}A \)
状态方程组: \( Q_{0}^{n+1}=D_0=\left( Q_{0}^{n}+Q_{1}^{n} \right) A, Q_{1}^{n+1}=D_1=\overline{Q_{0}^{n}}A \)
输出方程组: \( Y=\left( Q_0+Q_1 \right) \overline{A} \)
状态转换真值表/状态表:用表格描述触发器从现态到次态的转换过程和结果
由状态方程组和输出方程组(Y为当前输出值):
\( Q_1^n \)
\( Q_0^n \)
\( A \)
\( Q_1^{n+1} \)
\( Q_0^{n+1} \)
\( Y \)
0
0
0
0
0
0
0
0
1
1
0
0
0
1
0
0
0
1
0
1
1
0
1
0
1
0
0
0
0
1
1
0
1
1
1
0
1
1
0
0
0
1
1
1
1
0
1
0
更加集中化的表示 (\(a\sim d\)分别表示\( Q_1^nQ_0^n \)的四种状态) :
\( Q_1^{n+1}Q_0^{n+1}/Y \)
\( Q_1^nQ_0^n \)
\( A=0 \)
\( A=1 \)
00(a)
00(a)/0
10(c)/0
01(b)
00(a)/1
01(b)/0
10(c)
00(a)/1
11(d)/0
11(d)
00(a)/1
01(b)/0
状态图:信号流程图方式描述状态转换和结果
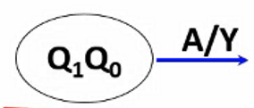
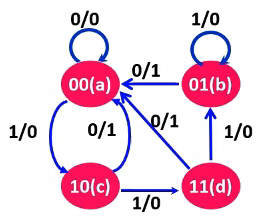
米利型输出
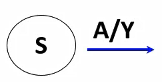
用圆圈表示状态,圆圈内描述状态值(名)
用箭头表示状态的转换方向
在箭头上标注输入输出值:输入条件/输出
输出:该状态下,输入A时Y的输出值
摩尔型输出
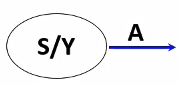
在箭头上标注状态转换条件
s是状态值(名),Y是该状态下Y的输出值
摩尔型+米利型
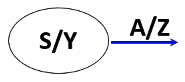
在箭头上标注状态转换条件/该状态下和该条件下Z的输出
s是状态值(名),Y是该状态下Y的输出值
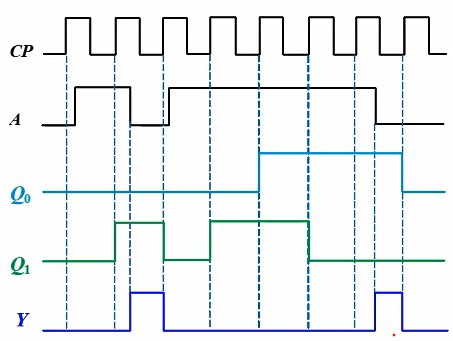
时序图:用波形图描述信号在时序上的对应关系(CP↑)
(出题: 给出CP和A,求\(Q_0\)、\(Q_1\)和Y)