第二章理想光学系统

通过对本章的学习，应：

理想光学系统的概念、成像性质、基点基面及其系统的表示；
1. 理想光学系统：对任意大的空间，以任意宽的光束都成完善像的光学系统，它具有“点对应点、直线对应直线、平面对应平面”的成像变换关系。物像这种对应关系称为共轭。表征理想光学系统的基本参数是基点和基面
2. 焦点、焦平面：与光轴上无限远点相共轭的点称为焦点。焦点有物方焦点和像方焦点之分。过物方或像方焦点垂直于光轴的平面，分别称为物方焦平面或像方焦平面。
3. 主点、主平面：垂轴放大率为+1的一对共轭平面称为主平面。主平面与光轴的交点称为主点。由主点到焦点的距离称为焦距。
4. 光学系统的物方焦距和像方焦距之间有如下关系：\( f'/f=−n'/n \)，式中，\( n' \) 为像方介质的折射率；\(n\) 为物方介质的折射率。当光学系统在同一介质中时，即 \(n'=n\)，则物像方焦距的绝对值相等，符号相反，有 \(f'=−f\)。
5. 节点、节平面：角放大率为+1的一对共轭平面称为节平面。它们与光轴的交点称为节点。经过节点的任何一对共轭光线互相平行。当光学系统在同一介质中时，系统的节平面与主平面重合。若光学系统物方折射率和像方折射率不等时，节平面与主平面不再重合，其位置关系由下式确定：\(x_J=f', x_J'=f\)。式中，\(x_J\)、\(x_J'\) 分别为从焦点\(F\)、\(F'\) 到节点\(J\)、\(J'\) 的距离。
6. 对理想光学系统而言，基点和基面的位置确定以后，系统的成像性质也就确定了。通常可用一对主平面和一对焦点来表示一个理想光学系统。
会用图解法和解析法求像，重点掌握高斯公式和牛顿公式及其理想光学系统的放大率公式；
1. 图解法求像：利用理想光学系统基点和基面的性质，通过作图法求物体在确定系统中的像。常用的光学性质有：
  1. 无限远轴上物点发出的光线一定通过像方焦点；
  2. 无限远轴外物点发出的光线一定通过像方焦面上一点；
  3. 物方焦点发出的光线经光学系统后平行于光轴；
  4. 物方焦面上一点发出的光线经光学系统后相互平行；
  5. 物方主平面上光线的人射高度与其共轭光线在像方主平面上的出射高度相等；
  6. 经过节点的任何一对共轭光线互相平行。
2. 理想光学系统的物像位置公式：
  1. 牛顿公式（以焦点为坐标原点）：\( xx'=ff' \)
  2. 高斯公式（以主点为坐标原点）：\( f'/l' + f/l = 1 \)。若光学系统位于同一介质（如空气）中，因为 \(f=f'\)，有：\( 1/l'-1/l=1/f' \)。
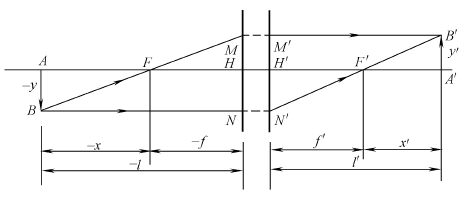
3. 理想光学系统的放大率：
  1. 垂轴放大率 \( \beta \)：
  \[ \beta = \frac{y'}{y} = -\frac{f}{x} = -\frac{x'}{f'} = -\frac{fl'}{f'l} = \frac{nl'}{n'l} \]
会灵活运用理想光学系统的组合公式求组合系统的焦距、基点和基面；
1. 两个理想光学系统的组合：若两个理想光学系统的焦距分别为 \(f_1'\) 和 \(f_2'\)（对应光焦度为 \(\Phi_1 = 1/f_1'\) 和 \(\Phi_2 = 1/f_2'\)），组合后系统的焦距、光焦度、焦点位置和主平面位置：
  
  \[f'=-\frac{f_1'f_2'}{\Delta}, f=\frac{f_1f_2}{\Delta}\]
  
  \[\Phi = \Phi_1 + \Phi_2 - d\Phi_1\Phi_2\]
  
  \[l_F' = f'\left(1 - \frac{d}{f_1'}\right), \quad l_F = -f\left(1 + \frac{d}{f_2}\right)\]
  
  \[l_H' = f' \frac{d}{f_1'}, \quad l_H = f \frac{d}{f_2}\]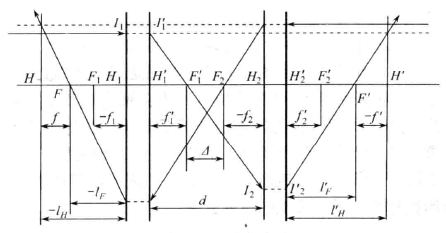
2. 当求 \( k \)（\(k \geq 3\)）个光组组合系统的参数时，往往使用如下正切计算法公式：
  
  \[\begin{split} \begin{cases} \tan U_1' = \tan U_2 = \frac{h_1}{f_1'} \\ h_2 = h_1 - d_1 \tan U_1' \\ \tan U_2' = \tan U_3 = \tan U_2 + \frac{h_2}{f_2'} \\ \vdots \\ h_k = h_{k-1} - d_{k-1} \tan U_{k-1}' \\ \tan U_k' = \tan U_k + \frac{h_k}{f_k'} \end{cases} \end{split}\]
  
  先求出 \(\tan U_k'\) 和 \(h_k\)，再代入公式：
  
  \[f' = \frac{h_1}{\tan U_k'}, \quad l_F' = \frac{h_k}{\tan U_k'}\]
  
  即可求出组合光学系统的焦距和焦点位置。式中，\(h_i\)、\(f_i'\)、\(U_i\)、\(U_i'\)、\(d_i\)（\(i = 1, 2, \ldots, k\)）分别为第 \(i\) 个理想光学系统的光线入射高度、焦距、物方孔径角、像方孔径角和它与后一个理想光学系统之间的间隔。
掌握两种典型的光组组合及其性质；
会求透镜的焦距、基点和基面位置，并了解透镜的分类和性质。
1. 透镜是构成光学系统的最基本单元。
2. 透镜的分类：
  1. 按照透镜对光线的作用可以分为两大类，一类对光线起会聚作用，它的光焦度 \( \Phi \) 为正值，称为会聚透镜或正透镜；另一类对光线起发散作用，它的光焦度 \( \Phi \) 为负值，称为发散透镜或负透镜。
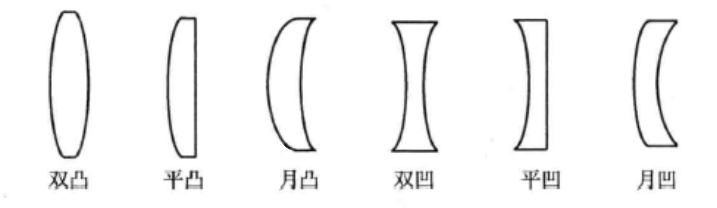
  2. 按照形状不同，透镜又可分为凸透镜和凹透镜两类，其中凸透镜包括双凸、平凸和月凸三种类型；凹透镜包括双凹、平凹和月凹三种类型。
  3. 凸透镜不一定都是正透镜，凹透镜也不一定都是负透镜，透镜的正负不仅与形状有关，还与透镜的厚度有关。
3. 在空气介质中，单个透镜的焦距表达式为：
  
  \[f' = \frac{nr_1 r_2}{(n-1) [n(r_2-r_1)+(n-1)d]}\]
  
  式中，\(n\) 为透镜的折射率；\(r_1\)、\(r_2\) 是透镜两个表面的曲率半径；\(d\) 为透镜的厚度。用透镜的光焦度来表示时，则有：
  
  \[\Phi = \frac{1}{f'} = (n-1)(\rho_1-\rho_2) + \frac{(n-1)^2}{n}d\rho_1\rho_2\]
  
  式中，\(\rho_1 = 1/r_1\)，\(\rho_2 = 1/r_2\) 分别为两个折射球面的曲率。
4. 当透镜的厚度与其焦距或曲率半径相比很小时，\(d\) 可略去不计。略去 \(d\) 的透镜称为薄透镜。此时有：\(\Phi = (n-1)(\rho_1-\rho_2)\)。对于单个薄透镜，两主面与球面顶点重合，其成像性质仅由焦距决定。

第二章 理想光学系统

第二章理想光学系统