第一章 几何光学的基本定律成像概念

通过对本章的学习，应掌握：

  1. 几何光学的基本定律

    1. 直线传播定律

    2. 独立传播定律

    3. 反射定律（\( I^{\prime\prime} = I \)）

    4. 折射定律（\( n' \sin I' = n \sin I \)）

  2. 光的全反射性质（入射角为 \( I = I_m \)，折射角 \( I' = 90^{\circ} \)，\( \sin I_m = n'/n \)）

  3. 费马原理、马吕斯定律以及二者与几何光学基本定律之间的关系

  4. 完善成像概念和相关表述

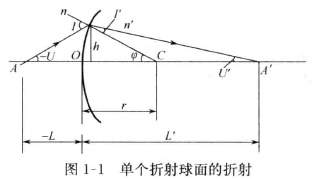
  5. 熟练应用符号规则进行单个折射球面的光线光路计算：\( \frac{n'}{l'} - \frac{n}{l} = \frac{n'-n}{r} \) （近轴区） image5

  6. 掌握单个折射球面和反射球面的成像公式

    1. 物像位置

    2. 垂轴放大率 \( \beta = \frac{y'}{y} = \frac{nl'}{n'l} \)

      1. \(\beta>0\) 成正像，物像位于系统同侧，虚实相反；\(\beta<0\) 成倒像，物像位于系统两侧，虚实相同；

      2. \(|\beta|>1\) 成放大像，反之成缩小像。

    3. 轴向放大率 \( \alpha \)

    4. 角放大率 \( \gamma \)

    5. 拉赫不变量

  7. 共轴球面系统的成像计算

\[\begin{split} \begin{cases} n_2 = n_1', & n_3 = n_2', \cdots & n_k = n_{k-1}' \\ u_2 = u_1', & u_3 = u_2', \cdots & u_k = u_{k-1}' \\ y_2 = y_1', & y_3 = y_2', \cdots & y_k = y_{k-1}' \end{cases} \end{split}\]
\[l_2 = l_1' - d_1, \quad l_3 = l_2' - d_2, \cdots \quad l_k = l_{k-1}' - d_{k-1}\]
\[h_2 = h_1 - d_1 u_1', \quad h_3 = h_2 - d_2 u_2', \cdots \quad h_k = h_{k-1} - d_{k-1} u_{k-1}'\]
\[n_1 u_1 y_1 = n_2 u_2 y_2 = \cdots = n_k u_k y_k = J\]